「新QC7つ道具」のマトリックスデータ解析法。それよりも汎用性のあるマトリックス分析を推奨します。

「新QC7つ道具」のマトリックスデータ解析法が主成分分析を使った数値データの解析法として広く紹介されているのを知り非常に驚きました。

30年以上の会社人生でそのような解析を行ったことは有りませんし、そもそも、しっかり理解するには数学や統計学の知識が必要不可欠です。誰でも気軽に扱えるようなものではありません。

それよりも、言語データを縦軸と横軸にとり、比較し数値化することで物事を分類し、考えるマトリックス分析は毎日のように使いますし、汎用性が高く、同じような効果が得られると思っています。

有名な所では仕事の優先順位を考える際に、重要度と緊急度の両面から考えるといった解析です。○○度と言われると何となく点数をつけやすくなり、個々の仕事を比較することで整理されて行きます。

私は数値データーを主成分分析を使って解析するマトリックスデータ解析法よりも、言語データをマトリックスで評価するマトリックス法の方を、日々の改善の道具として使う事を推薦します。

マトリックスデーター解析法を理解するために

重回帰

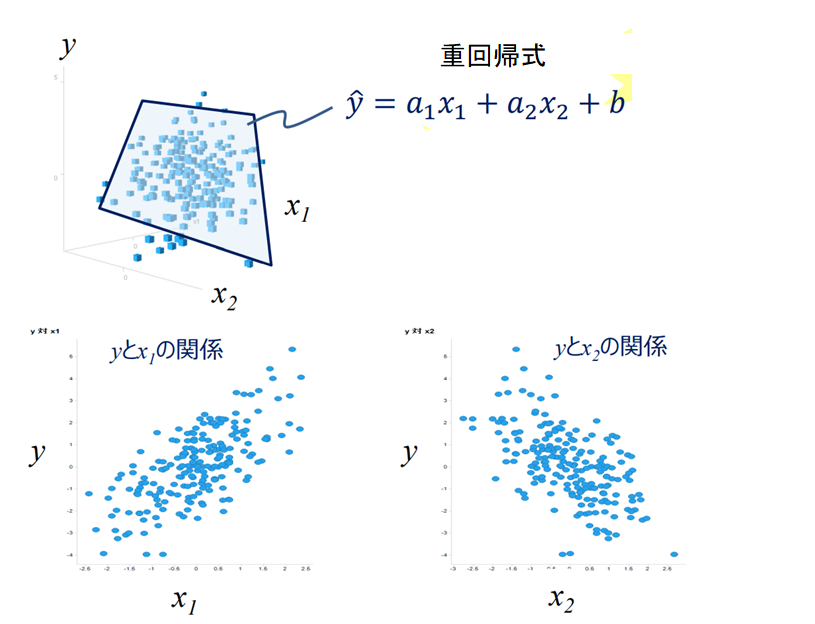
要因（説明変数）がX1だけであれば1次方程式で表されますが、X1、X2、と2種類以上になると重回帰と呼び、数学的には平面の方程式で示される形になります。

単回帰では直線の傾きはあまり意味を成しませんが、重回帰の場合、各変数の結果に与える影響を示すことになりますので、大事な指数となります。

しかし、この傾きはXが1だけ増えれば、Yはいくら変わるかを示しているので、単純に傾きがが大きければ影響が大きいとも言えません。データーを同じ土俵で評価できるように標準偏差で標準化することが必要になります。

数学的には1次か多次元かだけで違いはありませんし、実際にはエクセルを使って簡単に重回帰計算も出来ますが実際のデーターへの応用では注意が必要です。

重回帰で気を付ける事

個人的には説明変数を選ぶ際に気を付けていますが、選ぶ基準は、直感で選んでいます。心配なら、説明変数どおしの単回帰で相関を調べ、相関係数が0.4以下（やや相関がある程度）を目安にすれば良いと思います。（正確を期す場合は、相関係数では不十分で2変数間ではそんなに相関しないけど、3変数間だとお互い相関しあっているような場合もあり得ます。）

マトリックスデータ解析法

世間一般には？主成分分析の考え方を使って、影響力の大きい第一主成分と第二主成分を取って関係性を調べる手法のようです。

具体的なやり方はマトリックス・データ解析法 | 日本のものづくり～品質管理、生産管理、設備保全の解説　匠の知恵 (takuminotie.com)のIT教材の評価の主成分分析を行った例が分かりやすかったです。以下引用します。

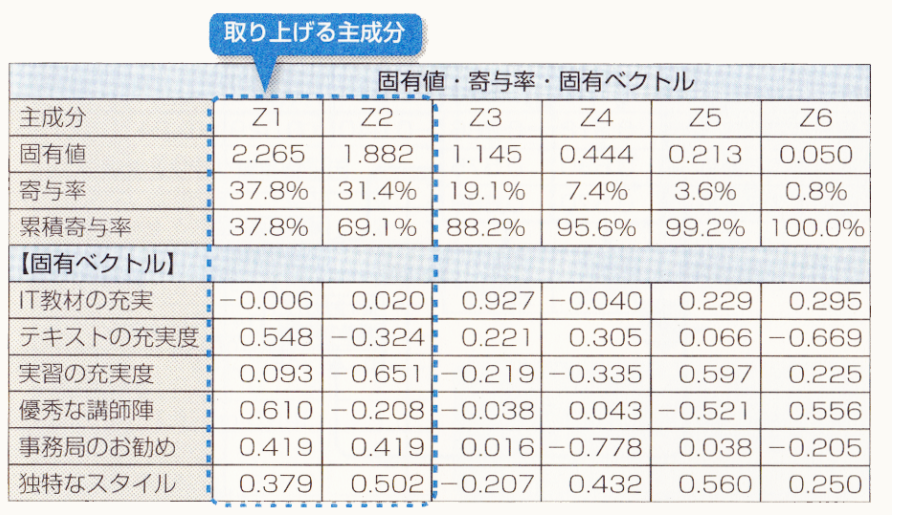
6っつあるIT教材の評価項目を「分散が最大になる方向」で情報が一番損なわれない方向の軸を考えると、Z1が第一主成分となり、相関が無いようにZ1と直交する方向で「分散が最大になる方向」で考えるとZ2が第二主成分となります。

Z2までの累積寄与率を見ると累積寄与率は69.1％ですので、全体の7割しか表現できていないとも言えます。この場合、Z3まで考慮して評価した方が良いかもしれません。

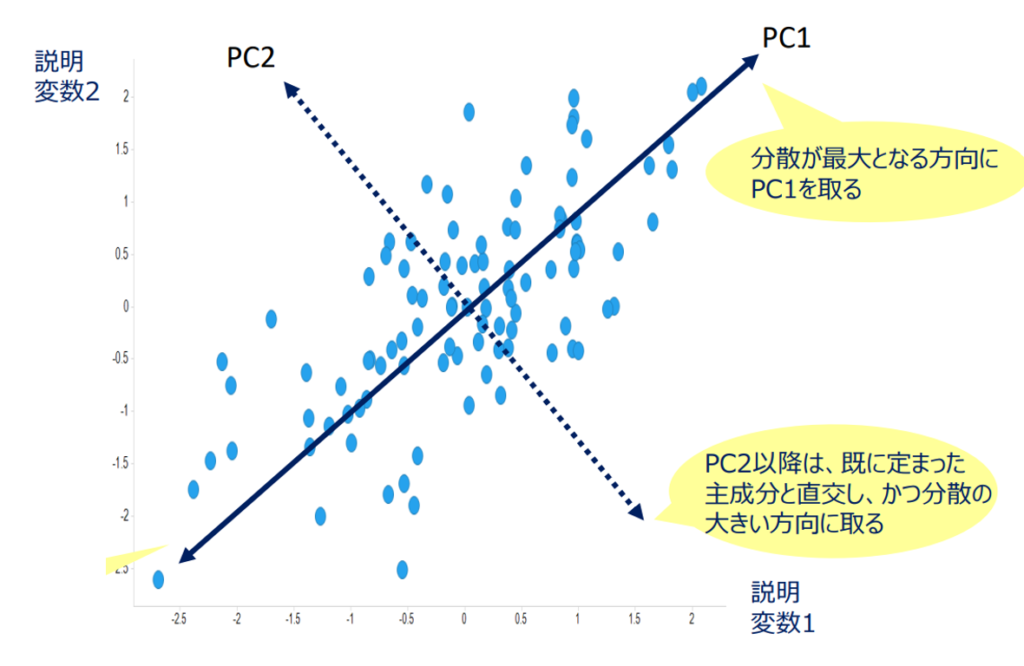
第一主成分と第二主成分に関しては下のグラフを参照ください。イメージしやすいかもしれません。

ここではPC1が上記のZ1、第一主成分に相当し、PC2がZ2、第二主成分に当たります。分散が最大となる方向を第一主成分とするのは、分散が多い方が情報がより多くなるからに他なりません。

固有値はバラツキの大きさを示しています。

垂直方向に第二成分を取るのは、第一成分との相関関係をなくすためです。垂直方向にとれば第一成分、第二成分は独立して変えられますが、垂直でなければ、第一成分と第二成分は連動して動いてしまいます。

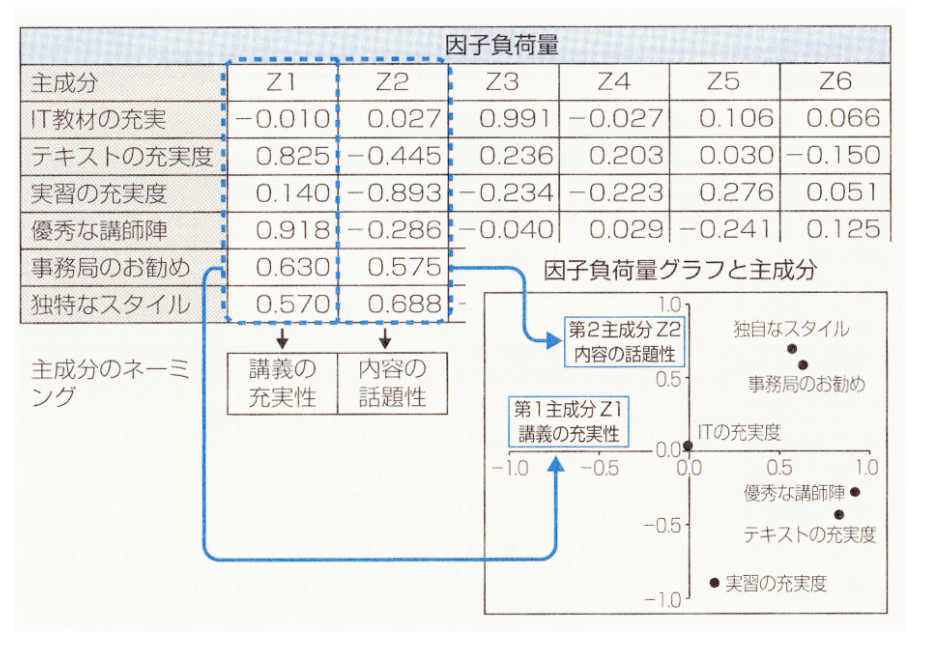
主成分分析の場合、数学的な、統計上の処理ですので、新たに設定した第一主成分と第二主成分には、ふさわしい名前をつける必要が有ります。

主成分分析は統計学上、データーを要約しただけですので内容は何を表しているのか？は分かりにくくなります。そのため因子負荷量を確認し、内容をよく吟味することが大切になります。

ここでは、第一主成分はIT教材はあまり充実していないけど、テキストが充実していて、講師陣も優秀なので「講議の充実性」と命名します。

第二主成分は独特なスタイルで事務局のおすすめなので「内容の話題性」と命名しました。

6っつの評価項目が、「講義の充実性」と「内容の話題性」で評価出来た事になります。

マトリックス分析

私は主成分分析は機械学習の話と関連して聞いたことは有りますが、普段の設計開発では使ったことはありません。

機械学習の方はそれこそデーターが何千となった場合、次元削減のために主成分分析を使うのは理解できますが、通常の品質改善に使う相関調査はそもそも重回帰もめったにやりません。普通は単回帰で十分です。（業種により違うかもしれません）

しかし、数値データーではなく、言語データの縦軸、横軸を決めてマトリックス表示にして考えて行く手法は一般的であり、また便利です。

例えば以下のようなものです。

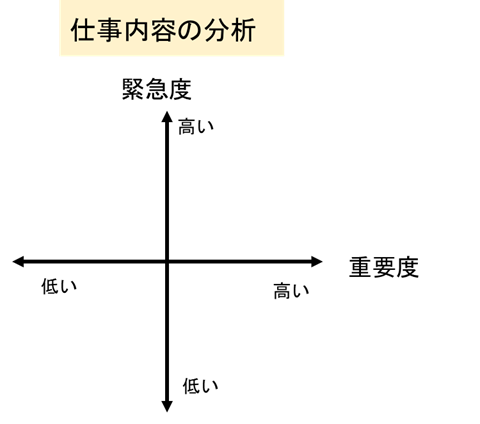
皆さん、仕事の優先順位を考えるとき、無意識に重要度と緊急度を考えて決めているのではないでしょうか？

まさしく、これがマトリックス分析です。皆さん、無意識にやられているのではないですか？

この仕事の重要度に点数をつければ？などと他の仕事と比較して点数をつけて行く方法です。

ちょっと待って、難易度や効果といった考え方も大切では？と思ったあなた。確かにその考えもありますよね。

しかし、難易度が高い、低いを考え得る際に緊急度と関係するところは有りませんか？

同じ仕事でも、1時間以内にしなければならないのと、1週間かけて完成させれば良い物では難易度は単純に時間をかけられる方が下がりますよね。

効果について考えれば、そもそも、重要度とかぶるところはないですか？効果があるとは重要度が高いので効果が有るとも言えますよね。難易度や効果も考慮して、緊急度、重要度を決めているとも言えます。まさしく多重共線性の問題です。

その場合、例えば、重要度が高く、緊急度も高い物を選んで、その中で優先順位をつける際に、難易度や効果といった切り口で考えると考えやすくないですか？。層別解析と呼ばれる手法の応用です。

逆に、効果が高くて難易度の高い物の中で、緊急度と重要度といった観点で優先順位をつけても良いです。

そういった意味では、数値データーのマトリックス解析も言語データのマトリックス解析も考え方は同じですが言語データの場合、課題（特性）を構成要素に分解し、掛け算で表せないか？つまり、中学生の時に数学で習った課題（特性）を因数分解する。といった考えが大切になります。

有名な所では、売り上げ高＝顧客単価X顧客数、自社の商品を単価と顧客数でみると、商品の位置づけも分かりやすくなり、戦略も立てやすくなります。

この考え方が、いわゆる主成分分析、つまりデータマトリックス回押せ紀宝を勝手に頭の中でやっているのと変わりありません。

通常の思考の中では、この言語データーを扱うマトリックス分析の方が遥かに汎用性が有ると思っています。

まとめ