「QC7つ道具」「新QC7つ道具」
数値データーを扱う「QC七つ道具」や言語データを扱う「新QC七つ道具」と呼ばれる物があります。項目としては以下のようになります。
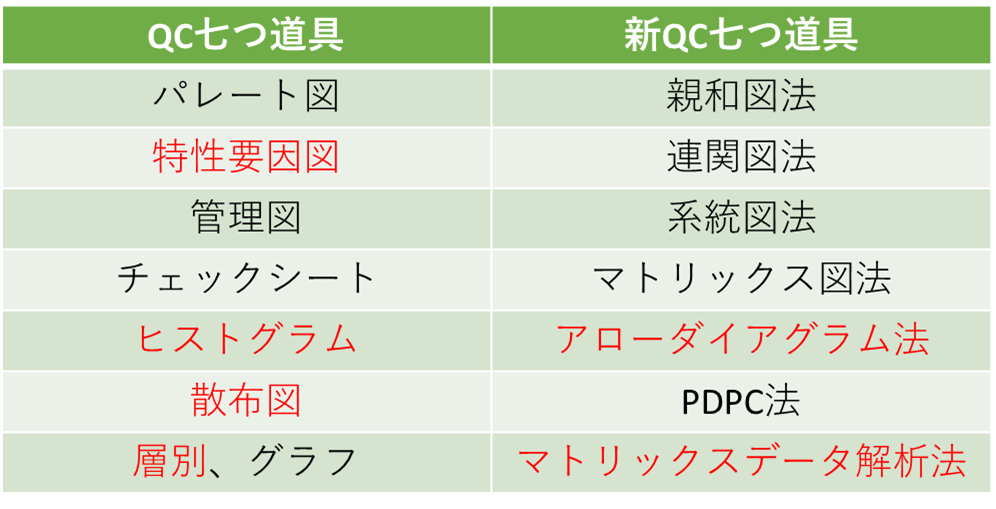
有名なので個々の詳細は他のサイトや本を参照いただければと思いますが、これらはまさしく道具です。何をする道具かと言えば、現象を見える化する道具です。
ここでは、赤字の項目でより使いやすそうな道具を紹介したり、使用上の注意点を紹介して行きたいと思います。
特性要因図
特性要因図/ロジックツリー
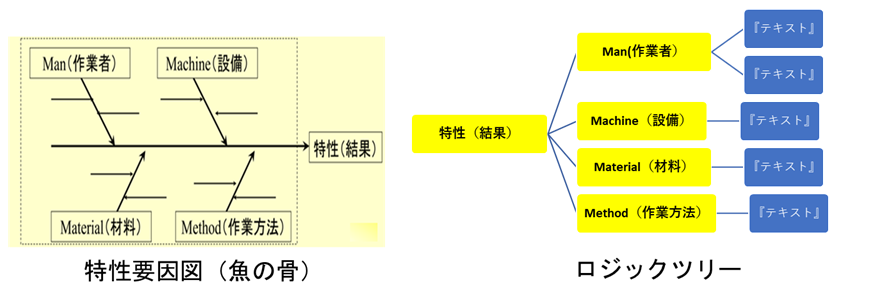
特性(結果)の原因と考えられる要因を出来るだけ多く、漏れ、ダブりなく洗い出すのが目的です。
従って網羅的に洗い出す必要があります。そのためにはブレンストーミング(質より量、批判厳禁、思い付き、便乗発言大歓迎)でどんどん書き出すのが良いです。
まとめ上げる道具としては、特性要因図(魚の骨)、ロジックツリーが知られています。
書き方の問題で思考法は同じです。特性要因図の方が全体としてのまとまりは感じますが、ブレストするとすぐに書くところがなくなるのでロジックツリーを個人的には多用しています。
FTA(故障の木)
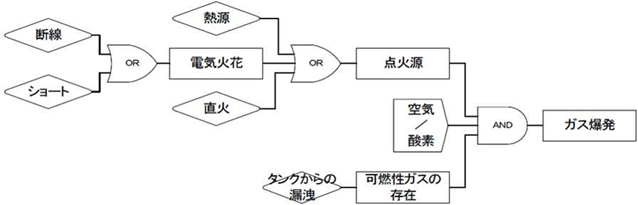
ガス爆発のFTAによる原因解析
上記のように、and or をつかって原因を解析して行く手法です。
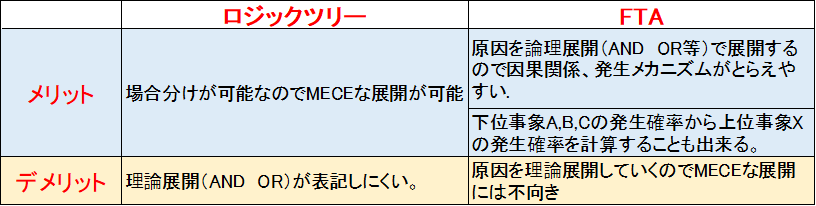
ロジックツリーとFTAのメリット/デメリット
ロジックツリー、FTAのメリット/デメリットを比較すると下の表のようなことが言えると思います。ケースバイケースで使い分ければ良いと思います。
ヒストグラム
正規分布のバラツキ
バラツキを示す指標として工程能力指数(Cp,Cpk)、標準偏差(σ)などが有りますが、あくまでも指標に過ぎません。
バラツキの原因を調査し、改善したいのならヒストグラムを作って分布の形を確認する事が大切です。
下記のサイトが説明としては分かりやすいと思います。
また、ヒストグラムも時間的には、ある限られた時間での結果です。時間による変化を見たいのならば管理図と併用して行く事になります。
ワイブル分布 ワイブル分布解析
工程能力指数や標準偏差は正規分布を前提としており、ヒストグラムも正規分布を前提として分布の形からバラツキの原因を探ろうとします。
一方,本質的に正規分布にならない品質特性もあります。有名な所では、機械が故障するまでの時間です。
ガラスの破壊強度も正規分布にはなりません。
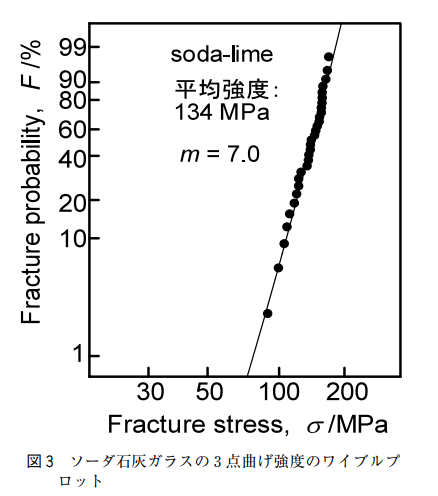
このような場合、左の図のようにワイブル分布解析(ワイブル確率紙、ワイブルプロットとしてまとめると分かりやすいです。
X軸は破壊強度を、Y軸は累積破壊確率を示しています。例えば、10%のガラスが割れるときの破壊応力はいくらか?(いわゆるB10)といった見方をします。
パラメータを適当に選ぶことで色々な分布に当てはめられる便利な考え方です。
ワイブルプロットにまとめると、上記の図のように直線に乗るようになり、その直線の傾きmをワイブル係数と呼びます。
- 傾きmが大きいと「バラツキ」は小さい。mが小さいと「バラツキ」が大きい
- 直線からずれているデータは「何らかの異常」か「別のモード」が起きている。原因調査が大切となる
層別
上述したように母集団の切り分け方の事ですが、4M、(人/物/機械/方法)が一般的。必要に応じて、E(環境)と言えますが、以下のような切り口が参考になると思います。

- 初めから細かく切り分けると、データー数も少なく、信憑性も下がり、逆に分かりにくい事も多いです。
- 大枠で目星をつけた上で、詳細な切り口に進んでデーター数を増やしていった方が良いと思います。
散布図、
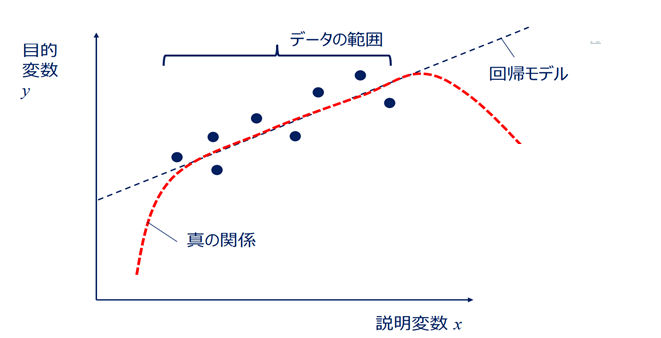
右の図のようにデータをX軸とY軸でプロットして関係性、分布を表すグラフを散布図と言います。
直線関係があれば1次方程式で近似され(右図の回帰モデル)相関係数r2などがエクセルで簡単に表記されます。
相関係数はデーターの相関性を表す指数で0.7以上あれば強い相関があると言われています。
関係性/相関=原因/因果関係とは限らない。
疑似相関とも呼ばれるようですね。別の第3の原因が両方に影響していれば見せかけの相関になります。ただ、そうは言っても相関が見られるということは重要ヒントである事には変わりありません。なぜ相関がみられるのか?といった観点で考えるのは大切です。
外挿、内挿は注意が必要
回帰モデルはあくまでもデーターから近似しているにすぎないので、データーの範囲外はどうなっているか不明です。製造条件のマージン評価では、どのぐらい、値がずれると線形モデルから外れるか?という事を調べる事が大切になってきます。
外挿、内挿は便利ですが、極力データー範囲を広く取る事を心がけましょう。
アローダイアグラム
アローグラム以外にガントチャートが有名です。
アローダイアグラムは見た目に分かりずらく、修正がしにくい。現実と計画を同時に表記しにくい。といった点が有り、私はガントチャートの方をよく使います。
良ければ下記の記事を参照ください。
マトリックスデータ解析法
私は数値データーを主成分分析を使って解析するマトリックスデータ解析法よりも、言語データをマトリックスで評価するマトリックス法を日々の改善の道具として使う事を推薦します。
良ければ以下の記事を参照ください。
まとめ
- 特性の要因を洗い出すには、特性要因図やFTA(故障の木)と呼ばれる手法がある。TPOに応じて適切なフレームラークを選択する事が大切になる。
- 正規分布のバラツキを考察するには標準偏差や工程能力指数よりもヒストグラムの分布の形を確認する事が大切である。
- 正規分布で表せないような分布に対してはワイブル分布を当てはめるのが有効である。
- アローダイアグラムはガントチャートに比べて作業のつながりは分かりやすいものの、修正しにくい、現実と計画の対比がしにくい。といった面がある。
- 数値データーを主成分分析を使って解析するマトリックスデータ解析法よりも、言語データをマトリックスで評価するマトリックス法の方が汎用性が有って便利。





コメント